合作客戶/
拜耳公司 |
同濟大學 |
聯合大學 |
美國保潔 |
美國強生 |
瑞士羅氏 |
相關新聞Info
推薦新聞Info
-
> 定性分析聚合物界面張力與系統黏度比之間的關系——數值仿真結果、結論
> 定性分析聚合物界面張力與系統黏度比之間的關系——數值模擬、實驗研究結果
> 定性分析聚合物界面張力與系統黏度比之間的關系——實驗部分
> 探究LB復合膜的酸致變色特性
> 受磷脂雙分子層啟發構建ZIBs兩性LB膜——制備高性能碘正極新思路
> 納米活性顆粒表面潤濕性測量方法及具體操作步驟
> 人工沖洗升級為超聲波清洗,可改善新能源電池沖壓配件的表面張力
> LB法組裝Silicalite-1型分子篩晶粒層,制備出高度b-軸取向的ZSM-5分子篩膜
> 微量天平高靈敏測定雞肉中磺胺類藥物含量
> 超低軌衛星環境效應研究也會用到超微量天平?
泡沫的微觀結構及演變動力學
來源:知乎阿黃sweetgirl 瀏覽 1071 次 發布時間:2022-06-17
前面有一篇短文中介紹了水中的自由氣泡的演變過程。然而,在實際生活中,我們見到和經常使用的卻是大量氣泡組成的泡沫。本文介紹一下泡沫的微觀結構靜力學及其演變過程分析。

泡沫一般結構如圖1所示,由于浮力作用,大量的氣泡漂浮在液體的表層,從上往下含有的氣泡的體積分數依次減小。在泡沫的研究中,把液體體積含量極少(通常少于1%)的泡沫成為干泡沫,把含量介于1%到約30%左右的泡沫成為濕泡沫。對于氣泡液體,幾乎所有的氣泡可以保持為球形,不用考慮氣泡之間直接接觸的氣泡膜問題,這不屬于泡沫物理學研究的范疇。如圖1所示,泡沫的結構尺度跨越10個數量級,從宏觀泡沫的演變規律,到微觀泡沫界面的穩定機制,對于泡沫的研究橫跨了物理,材料,界面化學等多個學科。
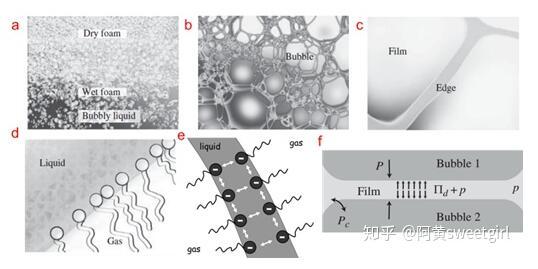
圖1.不同尺度下的泡沫結構及穩定機制(Ref 1)(a)整個泡沫結構,尺度為0.01 m至1 m。(b)干泡沫的放大部分,尺度為0.1 mm至1 cm。(c)液體通道,也叫Plateau邊界,尺度為1 um至0.1 mm以及肥皂泡膜,尺度為10 nm到1 um。(d)氣液界面的分子層結構,尺度為0.1 nm到10 nm。e-f)氣泡膜在界面靜電力排斥作用即楔裂壓(disjoining pressure)的作用下而穩定存在。
(1)泡沫的結構規律
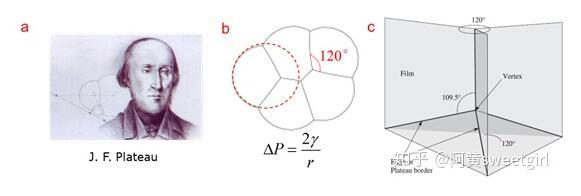
圖2 Plateau及其干泡沫靜態結構力學三定律(Ref 1)
泡沫物理學集中于研究泡沫的結構、靜力學、動態演變及排液等內容。它是一個十分古老的學科,由比利時物理學家Plateau在19世紀中葉開創(圖2a)。Plateau在數十年的失明的時光里,依舊通過指導他侄子做試驗,堅持研究肥皂泡薄膜的幾何形態及其背后隱藏的力學規律。1873年,他和侄子把自己的實驗現象和分析結果做了系統整理,以法文發表,從此把對泡沫結構的研究由定性印象推到了量化階段,開創了泡沫物理學(Ref 2)。在泡沫靜力學方面,Plateau的主要貢獻在于其提出了干泡沫的靜態結構力學的三定律,它是后續泡沫研究的基石:
1)膜力學平衡:肥皂膜是光滑的,它的曲率半徑是處處相等的,其大小可以用Laplace方程去計算。對于2維泡沫,每條氣泡邊界都是圓弧的一部分(圖2b);
2)邊力學平衡:三個肥皂膜相互接觸總是形成三條邊,且任意三條邊的夾角必須為120°(圖2b),此時力平衡并且體系能量最低。
3)頂點力學平衡:當四條邊在空間形成一個頂點時,此頂點處的四條邊任意兩條的夾角都為109.5°,只有這個角度才能使膜以120°角互相連接達到力平衡(圖2c)。
(2)泡沫的演變
Plateau的泡沫結構力學三定律對于后續泡沫的研究具有重要的意義。它直接引出了一系列有關氣泡的推論。
比如,依據Plateau第一定律,可以推出,相鄰三個相互接觸的氣泡的三條邊界上的曲率之和為零(Curvature sum rule)。其中最重要地是1952年von Neumann利用它推導出了二維泡沫的演變方程(Ref 3)。
推導二維泡沫的演變方程需要用到幾何荷數(Geometry charge)的概念。下面我們首先介紹一下幾何荷數的定義。
假設二維干泡沫中的任一氣泡如圖3b所示,氣泡的邊數為n,從a點開始,再回到a的邊長分別標記為l1到ln,每邊所對應的曲率為k1到kn(Plateau第一定律)。現在假設有一點從a點沿著邊向b運動,到b點時,所走的路徑為l1,轉動的角度為這條邊所對應的圓心角(向外為正,向內為負值),為k1*l1。此時要想繼續沿著邊運動,需要向內轉動π/3角度(根據Plateau第二定律),如圖3b所示。轉動后繼續運動,直到到達原來的點a。此過程,n條邊總共在頂點處轉動的角度為nπ/3,在邊上轉動的角度為
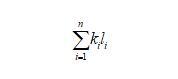
此點的運動方向變化總共為2π,可建立關系:
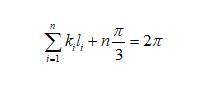
則幾何荷數q的定義為:
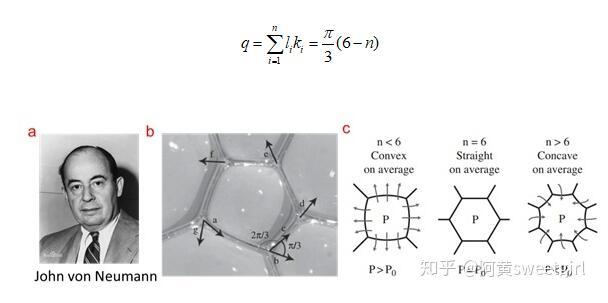
圖3 Von Neumann及二維干泡沫演化規律(Ref 1)
幾何荷數的含義即是每邊所對應的圓心角之和,其中對于氣泡而言往外凸起的邊為正值,往里凹下的邊其圓心角為負值。幾何荷數能夠反應出氣泡的平均凹凸程度,是對氣泡平均形貌的一個表征。通過公式可以看出,邊長大于6的氣泡平均是凹下的,邊長等于6的氣泡平均是平的,而變長小于6的氣泡,平均起來是凸起的,如圖3c所示。
下面我們推導二維泡沫的演變方程,由于任一氣泡跟周圍氣泡的氣體交換都是通過氣泡邊界進行的,則氣泡體積(二維氣泡用面積表示)隨時間的變化率跟邊界長度和邊界上的壓強差都有關系,可以表示為
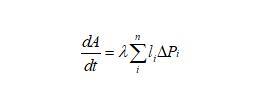
式中λ為氣體傳輸系數,根據Laplace方程可得
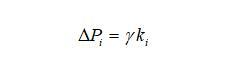
結合上式及上面q的推導過程公式,可得
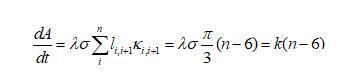
二維泡沫的演變方程表明,氣泡的變化只和其邊的個數有關,對于邊長大于6的氣泡,隨著演化體積會增大,邊長等于6的氣泡,其體積保持不變。而對于邊長小于6的氣泡,其體積會逐漸變小。注意,這兒體積保持不變,不代表氣泡不與外界發生氣體傳輸,只是表示進入氣泡和出去氣泡的體積是相等的,總體顯示體積顯示不變,也不代表氣泡的邊界不發生移動。
Von Neumann的二維演變方程的著名及其重要性是它不單單適用于二維泡沫,凡是具有網格結構的二維體系,界面移動受界面張力調控,其速率受界面曲率調控的情形都可以用這個方程去表達。這種情形在自然界中是十分普遍的,比如如水上面油脂分子層的演化、熔化時晶界的變化、冰晶的生長等(Ref 5,Ref 6)。
自從Von Neumann推出了二維泡沫的演變方程以來,人們一直希望能推導出三維泡沫的演變方程,直到50多年后的2007年,美國葉史瓦大學MacPherson等在Nature上發表了一篇題為“把von Neumann方程拓展到三維微結構粗化的研究”(The von Neumann relation generalized to coarsening of three-dimensional microstructures)的論文,完成了對三維泡沫體系演變方程的推導(Ref 7)。之后,加利福尼亞大學的Saye等于2013年在Science上發表論文,從模擬上實現了三維泡沫的結構重排、排液、破裂等一系列過程(圖4),在泡沫演變歷史上具有劃時代的意義(Ref 4)。至此,人們對泡沫演變的規律得到了充分的認識。

圖4目前對三維干泡沫演變的模擬研究65
Ref 1:I.Cantat,S.et al.Foams:Structure and Dynamics.Oxford University Press,Oxford,(20
Ref 1:I.Cantat,S.et al.Foams:Structure and Dynamics.Oxford University Press,Oxford,(2013).
Ref2:孫其誠&譚靚慧.泡沫物理學史拾萃.物理37,473-481(2008).
Ref3:Neumann,J.v.in Metal Interfaces(ed.Herring,C.),108-110(Americal Society for Metals,Cleveland,1952).
Ref 4:Saye,R.I.&Sethian,a.J.A.Multiscale Modeling of Membrane Rearrangement,Drainage,and Rupture in Evolving Foams.Science 340,720(2013).
Ref 5:Stavans,J.The evolution of cellular structures.Rep.Prog.Phys.56,733-789(1993).
Ref 6 Glazier,J.A.&Weaire,D.the kinetics of cellular patterns.J.Phys.:Condens.Matter 4,1867-1894(1992).
Ref 7:MacPherson,R.D.&Srolovitz,D.J.The von Neumann relation generalized to coarsening of three-dimensional microstructures.Nature 446,1053-1055(2007).
注:本文節選自本人博士畢業論文前言部分。










