合作客戶/
拜耳公司 |
同濟大學 |
聯合大學 |
美國保潔 |
美國強生 |
瑞士羅氏 |
相關新聞Info
推薦新聞Info
-
> 定性分析聚合物界面張力與系統黏度比之間的關系——數值仿真結果、結論
> 定性分析聚合物界面張力與系統黏度比之間的關系——數值模擬、實驗研究結果
> 定性分析聚合物界面張力與系統黏度比之間的關系——實驗部分
> 探究LB復合膜的酸致變色特性
> 受磷脂雙分子層啟發構建ZIBs兩性LB膜——制備高性能碘正極新思路
> 納米活性顆粒表面潤濕性測量方法及具體操作步驟
> 人工沖洗升級為超聲波清洗,可改善新能源電池沖壓配件的表面張力
> LB法組裝Silicalite-1型分子篩晶粒層,制備出高度b-軸取向的ZSM-5分子篩膜
> 微量天平高靈敏測定雞肉中磺胺類藥物含量
> 超低軌衛星環境效應研究也會用到超微量天平?
正丁醇水溶液表面張力的測定原理及計算過程
來源:大學化學 瀏覽 163 次 發布時間:2024-06-13
借助MATLAB工程計算平臺,通過程序設計完成了“正丁醇水溶液表面張力的測定”應用軟件的開發。在完成錄入壓差實驗數據后,不僅可以自動計算和填入溶液的表面張力,還能夠實現溶液表面張力與濃度定量關系的希斯科夫斯基經驗方程(Szyszkowski′s equation)中待估參數的求解,并用以求導供給吉布斯公式計算溶液的吸附量,進而推算溶液飽和吸附量和正丁醇分子的截面積。軟件的操作過程簡便、直觀、高效,避免了人工數據處理、繪圖的煩瑣和人為誤差,可提高實驗結果的準確性和重現性。
1、表面張力測定原理
表面張力是流體的重要物性數據,與諸多工業領域應用聯系密切,如化工傳質分離、食品藥品加工、礦物浮選、制冷工程等,但表面張力無法直接通過熱力學微分關系式從狀態方程導出,精確可靠的表面張力數據只能通過實驗精密測量得到,常用方法包括毛細管上升法、最大氣泡壓力法、掛環法、滴體積法等靜力學法和震蕩射流法、毛細管波法等動力學法[1]。
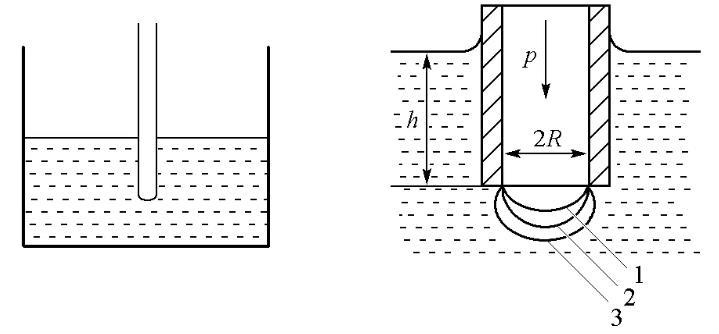
圖1表面張力的泡壓法測定原理圖
由于最大氣泡壓力法的器材易得,且易于學生理解表面張力的原理,因而一直是教學中測定液體表面張力的一種常用方法[2]。如圖1所示,測定時將一根毛細管插入待測液體內部,從管中緩慢地通入惰性氣體對其內的液體施以壓力,使管端形成氣泡逸出。當所用的毛細管管徑較小時,可以假定所產生的氣泡是球面的一部分;但是在氣泡生成及發展過程中,氣泡的曲率半徑會隨惰性氣體的壓力變化而改變。當氣泡的形狀恰為半球形時,氣泡的曲率半徑最小(即毛細管半徑R),此時根據Laplace方程,管內外壓差達最大,其值Δpmax=p-ρgh可由差壓計測量得到[3]。利用最大壓差和毛細管半徑即可計算表面張力σ:
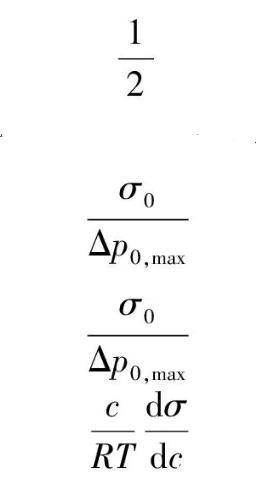
若采用同一支毛細管和差壓計,在相同溫度下測定已知表面張力的液體(如25℃蒸餾水,σ0=71.97mN·m-1)在毛細管中的最大壓差Δp0,max,則有:
針對實驗采集與計算獲得有限多個不同濃度c下的表面張力σ,傳統的數據處理方法是手工繪制這些離散點的趨勢曲線,并求出曲線上指定幾個點的切線斜率,進而求算表面吸附量。然而,手工圖解作切線這一步的誤差較大,結果重復性差,難以得到準確的結果。對此,本文介紹在物理化學實驗“正丁醇水溶液表面張力的測定”中,借助MATLAB工程計算平臺[5],選擇希斯科夫斯基關聯方程(Szyszkowski′s equation),經由少數測量數據點關聯與求解正丁醇溶液表面張力和濃度之間的定量關系數學模型,并借此求算曲線上任意指定濃度下的切線斜率,進而求算該濃度下的表面吸附量,以提高數據處理的效率和質量。
2、實驗部分
2.1儀器及試劑
儀器:AF-02型數字式微壓測量儀,數控恒溫槽,5mL和10mL移液管各一支,堿式滴定管1支,50mL容量瓶9個,樣品管1個,毛細管1個,抽氣瓶1個,錐形瓶1個,玻璃漏斗1個。
試劑:正丁醇(A.R.)及其不同濃度的標準溶液。
2.2實驗步驟
①用體積法準確配置濃度為0.025、0.050、0.075、0.10、0.15、0.20、0.25mol/L的正丁醇水溶液各50mL。
②如圖2示,調節恒溫槽的溫度在25℃,打開AF-02型數字式微壓式測量儀的電源,預熱20min。
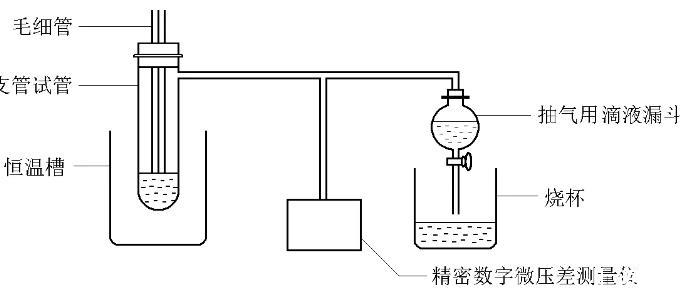
圖2表面張力測定的實驗裝置
③先用洗液洗凈大試管與毛細管,再用自來水和蒸餾水洗凈;在大試管中注入適量蒸餾水,使毛細管端口剛好與液面垂直相切;將大試管安裝在恒溫水溶液內,用小漏斗給抽氣瓶裝滿自來水。
④連接好裝置,使其無漏氣。在體系通大氣的條件下按校零按鈕,使顯示器值為0.000kPa。
⑤測定蒸餾水的Δp0,max。打開抽氣瓶的活塞,使瓶內水緩慢滴出,導致大試管逐步減壓,待氣泡形成速度穩定(約5~10秒出一個氣泡)后,讀出氣泡脫出瞬間的Δp0,max;連續讀3次,取平均值。
⑥按照上述方法測定不同濃度正丁醇溶液的Δpmax值。不同溶液測定時須按低濃度到高濃度的次序測定;測定每一樣品時只需要用同樣濃度的溶液淌洗3次即可,并對測量數據進行記錄(例見表1)。
⑦實驗完畢,清洗玻璃儀器,整理實驗臺。
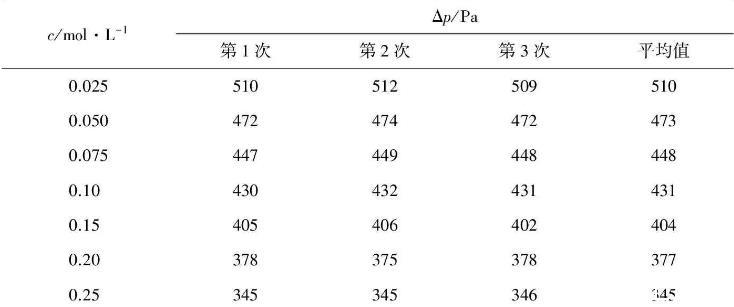
表1不同濃度正丁醇水溶液的表面張力測定數據
3、實驗數據處理及MATLAB實現
3.1表面張力的希斯科夫斯基經驗方程
考慮到正丁醇系短鏈醇、醛、酮、酸、胺等第二類表面活性物質,在低濃度下其表面張力隨濃度增大在起始時降得較快、隨后呈減慢的特點,適宜選用希斯科夫斯基經驗方程來擬合溶液表面張力σ與溶液濃度c之間的非線性關系[6]。
式中σ0為溶劑蒸餾水的表面張力,α和β為物系待估計的模型參數。
3.2飽和吸附量和溶質分子截面積的計算
在一定溫度下,吸附量Γ與溶液濃度c的關系可由Langmuir單分子層等溫吸附式表示[7]。
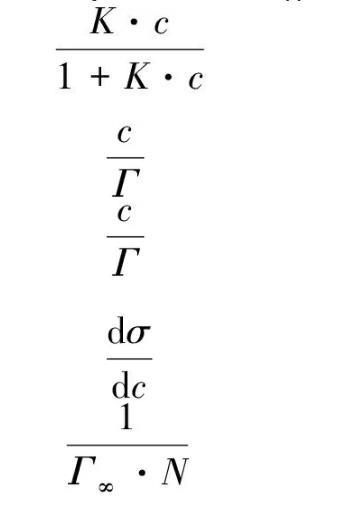
式中N為阿伏加德羅常數。
3.3用MATLAB實現表面張力及表面吸附量的計算
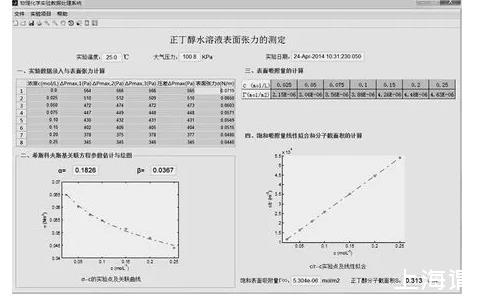
圖3所示的“正丁醇水溶液表面張力的測定”實驗數據處理軟件由4個單元模塊構成:①實驗數據錄入和溶液表面張力的程序自動計算;②表面張力與濃度關聯的希斯科夫斯基經驗方程的參數估計與圖形繪制;③基于吉布斯公式完成溶液表面吸附量的計算;④飽和吸附量的線性回歸求解及正丁醇分子截面積的計算。
在第一步的數據錄入表格過程中,當完成第一行c=0.0的蒸餾水3次壓差平行測定數據后,軟件將自動完成其平均壓差的計算和自動填充,然后在錄入物性手冊中查得25℃蒸餾水的表面張力為0.07197N·m-1,毛細管常數λ將由程序算出,并作為程序內存變量用于數據表格中不同濃度溶液的表面張力σ的計算。
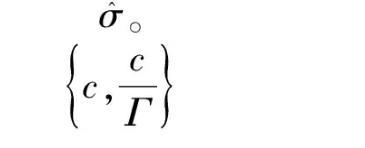
4、結論
正丁醇是表面活性物質,其表面吸附量隨溶液濃度增大升高,并最終趨于飽和吸附。在本實驗的數據處理上,選用希斯科夫斯基經驗方程進行關聯與擬合,通過Gibbs吸附等溫式計算溶液吸附量,通過線性回歸計算飽和吸附量,計算結果符合理論情況,可以較好地反映正丁醇溶液的特性。另外,在數據處理的最后步驟中,正丁醇分子截面積的計算結果也與文獻值吻合較好,能滿足實驗精度要求。
基于MATLAB工程計算平臺開發設計的“正丁醇水溶液表面張力的測定”應用軟件可用于進行實驗數據計算和繪圖,可以快速、客觀地得到實驗結果,避免了手動作圖的主觀性和人為誤差。










